The Birthday Paradox
A look at the birthday paradox
Try It Yourself
Theory and Computation
It is easier to determine the probability of no one having their birthday on the same day as someone else. For simplicity, we disregard the facts that there may be twins and that more births occur in certain months. Additionally, we also assume that every year has 366 days.Let's look at a group of five people. It is easiest to look at the people one by one: the first person has their birthday on a certain date. The probability that the second person's birthday isn't on that same day is 365/366. The third person will have a probability of 364/366 that he hasn't got his birthday the same day as the two other people we've looked at (since two dates are already "occupied"). Thus, the more people we have, the smaller the probability becomes that their birthday isn't on the same date as someone else's. The probability of there not being any shared birthday date in a group of 5 people is as follows:
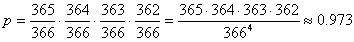
This means that the probability of there not being any same-day birthdays with 5 randomly chosen people is 97,3%. If we invert this, we get the probability of there being same-day birthdays: 1 - 0,973 = 0,027 ≘ 2,7%. The probability for this 5-person situation seems intuitive, but it grows rapidly: within a group of 20 people, the probability of there being at least one pair having their birthday the same day is 41%, which — keeping in mind that there are 366 possible days — is a lot!
You can calculate the probability of there being same-day, same-week or same-month birthdates within a given number of people above.
For further reading (and graphs), please look at the Birthday problem article on Wikipedia.